[DSA] 2. Searching algorithm
[DSA] 1. Computation Complexity와 Big-OAlgorithm?(Generally) 어떤 문제를 해결하기 위한 일련의 계산 절차.(Computer science에서는) 컴퓨터 상에서 돌아가는 program의 mathematical abstraction. Efficiency of an Algorithm어떤
jae-walker.tistory.com
[DSA] 3. Iteration vs. Recursion
[DSA] 2. Searching algorithm이전글 : 2025.04.13 - [Data Science] - [DSA] 1. Computation Complexity와 Big-O [DSA] 1. Computation Complexity와 Big-OAlgorithm?(Generally) 어떤 문제를 해결하기 위한 일련의 계산 절차.(Computer science에
jae-walker.tistory.com
이전 글에서는 Searching algorithm 2가지에 대해서 동작을 설명하고, Big-O를 계산해보는 내용을 포스팅했다. 추가적으로, 알고리즘의 반복 연산을 구현하는 2가지 방법에 대해서도 알아보았다.
이번에는 Searching 다음으로 자주 쓰이는 기본적인 알고리즘, "Sorting"에 대해 다뤄본다.
Sorting algorithm
Sorting은 N개의 값을 가지는 데이터를 monotonically (단조적으로) 증가하거나 감소하도록 순서를 재정렬하는 동작이다. 예를 들어, 아래와 같은 input array를 ascending order로 정렬하면 아래의 sorted array가 나오도록 값들을 재정렬한다.
input = [1, 4, 6, -1, 5, -8, 12]
sorted = [-8, -1, 1, 4, 5, 6, 12]
Sorting이 필요한 이유는, 값들이 무작위로 배열되어 있는 것보다 일정 순서로 정렬되어 있을 때 data 분석이 더 용이하고 문제를 단순화(예를 들어, 앞에서 봤던 binary search) 할 수 있기 때문이다.
1. Insertion Sort
list를 sorted region과 unsorted region으로 나누고 unsorted region에 있는 element들을 앞에서부터 하나씩 sorted region의 적절한 자리에 넣는 방식. 손에 카드를 들고 왼쪽에서부터 하나씩 정렬하는 방법을 생각하면 된다.
python 코드로 구현하면 아래와 같다.
def insertion_sort(list):
for unsorted_start in range(1, len(list)): # sorted/unsorted boundary
key = list[unsorted_start] # unsorted_start에 있는 값을 꺼내 저장
j = unsorted_start - 1
print(f"{list[:unsorted_start]} | {key} | {list[unsorted_start+1:]}")
while j >= 0 and key < list[j]: # sorted 뒤쪽에서부터 key값보다 크면,
list[j+1] = list[j] # 값들을 하나씩 뒤로 밀고
j -= 1
list[j+1] = key # 작은 값이 나오면 그 자리에 key 값을 insert# output : [sorted_region] | {key} | [unsorted_region]
[-7] | 15 | [2, 6, -1, 5, 4, 10, -4, 21]
[-7, 15] | 2 | [6, -1, 5, 4, 10, -4, 21]
[-7, 2, 15] | 6 | [-1, 5, 4, 10, -4, 21]
[-7, 2, 6, 15] | -1 | [5, 4, 10, -4, 21]
[-7, -1, 2, 6, 15] | 5 | [4, 10, -4, 21]
[-7, -1, 2, 5, 6, 15] | 4 | [10, -4, 21]
[-7, -1, 2, 4, 5, 6, 15] | 10 | [-4, 21]
[-7, -1, 2, 4, 5, 6, 10, 15] | -4 | [21]
[-7, -4, -1, 2, 4, 5, 6, 10, 15] | 21 | []
Time complexity
Insertion sort의 time complexity를 따져 보자. 먼저, Insertion 대상이 되는 key값을 고르는 loop를 최대 N-1 돌아야 하니 O(N)이고, key값이 들어갈 자리를 찾아 넣기 위한 loop 또한 최대 N-2 돌아야 하니 O(N)이다. 그리고 이 loop는 중첩되어 있으므로, O(N^2)이 된다.
2. Selection Sort
Insertion Sort가 unsorted region의 값을 sorted region의 적절한 자리에 넣는 방식이라면, selection sort는 반대로 unsorted region에서 가장 작은 값을 찾아 sort region으로 옮기는 방식이다. sorted region으로 일단 옮기고 거기서 자리를 찾을 것이냐, unsorted region에서 먼저 옮길만한 놈을 찾고 옮길 것이냐의 차이.
def selection_sort(list):
for unsorted_start in range(len(list)): # sorted/unsorted boundary
min = unsorted_start # sorted로 옮길 값을 제일 앞에 있는 값으로 초기화
print(f"{list[:unsorted_start]} | {list[unsorted_start:]}")
for j in range(unsorted_start+1, len(list)): #unsorted에 있는 나머지 값들과
if list[j] < list[min]: # 크기를 비교해서 min값을 찾음
min = j
# min과 unsorted_start 값을 swap
list[unsorted_start], list[min] = list[min], list[unsorted_start]# output : [sorted_region] | {key} | [unsorted_region]
[] | [-7, 15, 2, 6, -1, 5, 4, 10, -4, 21]
[-7] | [15, 2, 6, -1, 5, 4, 10, -4, 21]
[-7, -4] | [2, 6, -1, 5, 4, 10, 15, 21]
[-7, -4, -1] | [6, 2, 5, 4, 10, 15, 21]
[-7, -4, -1, 2] | [6, 5, 4, 10, 15, 21]
[-7, -4, -1, 2, 4] | [5, 6, 10, 15, 21]
[-7, -4, -1, 2, 4, 5] | [6, 10, 15, 21]
[-7, -4, -1, 2, 4, 5, 6] | [10, 15, 21]
[-7, -4, -1, 2, 4, 5, 6, 10] | [15, 21]
[-7, -4, -1, 2, 4, 5, 6, 10, 15] | [21]
smallest값을 sorted로 옮기고 난 다음에는 1개 적어진 unsorted region에서 같은 동작이 반복되는 형태임을 알 수 있다. 오? smaller scale의 sub-problem을 가지는 형태? recursion으로도 구현할 수 있는 조건이다! recursion으로도 한 번 구현해보자.
def selection_sort_recr(list, unsorted_start=0):
# base case
if unsorted_start > len(list) - 1:
return
# general case
min = unsorted_start
print(f"list[:unsorted_start]} | {list[unsorted_start:}")
for j in range(unsorted_start + 1, len(list)):
if list[j] < list[min]:
min = j
list[unsorted_start], list[min] = list[min], list[unsorted_start]
selection_sort_recr(list, unsorted_start + 1) # sub-problem call
Time complexity
Selection sort의 time complexity도 따져 보자. 먼저, unsorted region에서 최소값을 찾기 위해 비교해야 하는 loop가 worst case에서 N-1 돌아야 하니 O(N)이고, select한 값을 sorted region으로 옮기는 동작을 최대 N만큼 해야 하니 O(N). 그리고 이 loop는 중첩되어 있으므로, O(N^2)이 된다. iteration이던 recursion이던 동일하다.
Insertion sort와 Selection sort는 동작만 약간 다를 뿐, 둘다 O(N^2)를 가진다. 흠... Big-O 포스트에서 봤던 그래프를 떠올려보면, O(N^2)은 시뻘건 horrible 영역에 있던 위험한 놈이었다. 데이터가 몇 개 없다면 그냥 돌려도 돌아는 가겠지만, 데이터가 많아질수록 답이 없어진다.
그래서 똑똑하신 분들께서 더 작은 time complexity로도 같은 sorting 문제를 풀 수 있는 방법을 몇 가지 찾아 놓으셨는데...
3. Merge sort
"Divide and Conquer" 방식으로 time complexity를 낮출 수 있는 대표적인 예시이다. (그래서 sorting에 들어가기에 앞서 뜬금없이 recursion이 나오나보다...ㅎㅎ)
Merge sort는 list를 sub-list로 나눈(divide) 다음, 각각의 sub-list끼리 sorting하고 합치는(conquer) 방식이다. 아래 그림은 2-way merge sort의 예시이다.

- Divide : List를 base case에 도달할 때까지 계속 반으로 나눈다. (2-way이므로 2개의 sub-list로 나누는 것이고, 몇 조각으로 나누냐에 따라 3-way, 4-way로도 할 수 있다.)
- Base case : element가 1개인 경우, 자기 자신을 return한다.
- Conquer : 하위 sub-list를 order에 맞게 합쳐서(merge) 상위 list를 만들어 나간다.
merge sort가 효율적인 알고리즘이 될 수 있는 것은 "merge" 방법에 있다. sub-list는 항상 자기들끼리는 sorting되어 있는 상태로 상위 list에 merge된다는 특성을 이용하여 time complexity를 낮출 수 있다. Base case부터 merge해나가는 과정을 살펴보자.
len(sub-list) == 1 , (각 sub-list의 가장 작은 값끼리 비교 후 상위 list로 merge) 2회 x sub-problem (N/2)개 = O(N)
len(sub-list) == 2 , (각 sub-list의 가장 작은 값끼리 비교 후 상위 list에 merge) 4회 x sub-problem (N/4)개 = O(N)
...
len(sub-list) == len(list), (각 sub-list의 가장 작은 값끼리 비교 후 상위 list에 merge) 4회 x sub-problem (N/4)개 = O(N)
Time complexity
정리하면, O(N) 연산을 merge depth 만큼 반복하게 되고, 2-way로 나눠나가므로 mergep depth는 log_2 N이다. 따라서, merge sort의 time complexity는 O(N logN)이 된다! 같은 sorting problem을 해결하는데 O(N^2)가 필요했던 insertion sort나 selection sort에 비해 time complexity가 확실히 줄어든다.
python code로 구현해보면,
def merge_sort(list):
# base case
if len(list) < 2:
return list
# general case
else:
# divide
mid = len(list) // 2
left = merge_sort(list[:mid])
right = merge_sort(list[mid:])
# conquer
merged = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] <= right [j]:
merged.append(left[i])
i += 1
else:
merged.append(right[j])
j += 1
merged.extend(left[i:])
merged.extend(right[j:])
return merged
Can it be better?
O(N^2)에서 O(N logN)으로 줄여보니 이런 궁금증이 든다. Complexity를 더 줄일 수도 있을까? 결론부터 말하면, Yes!
binary search가 sorted list라는 전제조건하에 O(N)에서 O(logN)으로 complexity를 줄일 수 있었던 것처럼, sorting도 특정 전제조건이 만족된다면 최대 O(N)까지 줄일 수 있다. 다만, O(N)보다 더 작아질 수는 없다. 직관적으로 봐도, sorting을 하려면 일단 전체 원소를 어떤 방식으로든 한번씩 확인해야 하는데 이 때 이미 O(N)이 필요하기 때문이다.
추가적으로, 값을 비교하며 정렬하는 comparison-based sorting의 best complexity는 수학적으로 O(N log N)이 된다고 한다. (증명이 궁금하신 분은... https://ilyasergey.net/YSC2229/week-04b_sorting_best_worst.html)
4. Counting Sort
앞에서 말한 것처럼, 특정 전제조건 하에서 O(N)만으로 sorting을 할 수 있는 알고리즘을 Linear-time Sort이라고 한다. 그리고 그 대표적인 예시 중 하나가 바로 counting sort이다.
전제조건
linear-time sort들이 가지는 전제조건은 보통 data 값이 제한된 범위의 정수값이거나, 분포가 고정되어 있는 실수값으로 한정된다. 그래야 data 내의 값들을 서로 비교하지 않고 숫자값 자체만 보고 어느 곳에 들어가야 하는지 바로 알 수 있기 때문이다.
Counting sort는 data element들이 0 ~ K인 정수로만 이루어져 있을 때 사용할 수 있다.
정렬 방식은 다음과 같다.
- Counting : 길이가 K이고 모든 값이 0으로 초기화된 count array를 만든 다음, input data를 하나씩 확인하여 해당 값을 index로 가지는 count array를 1씩 증가시킨다.

- Accumulation : 모든 값을 확인한 다음, count array의 index를 각 count 값만큼 반복하여 누적한다.
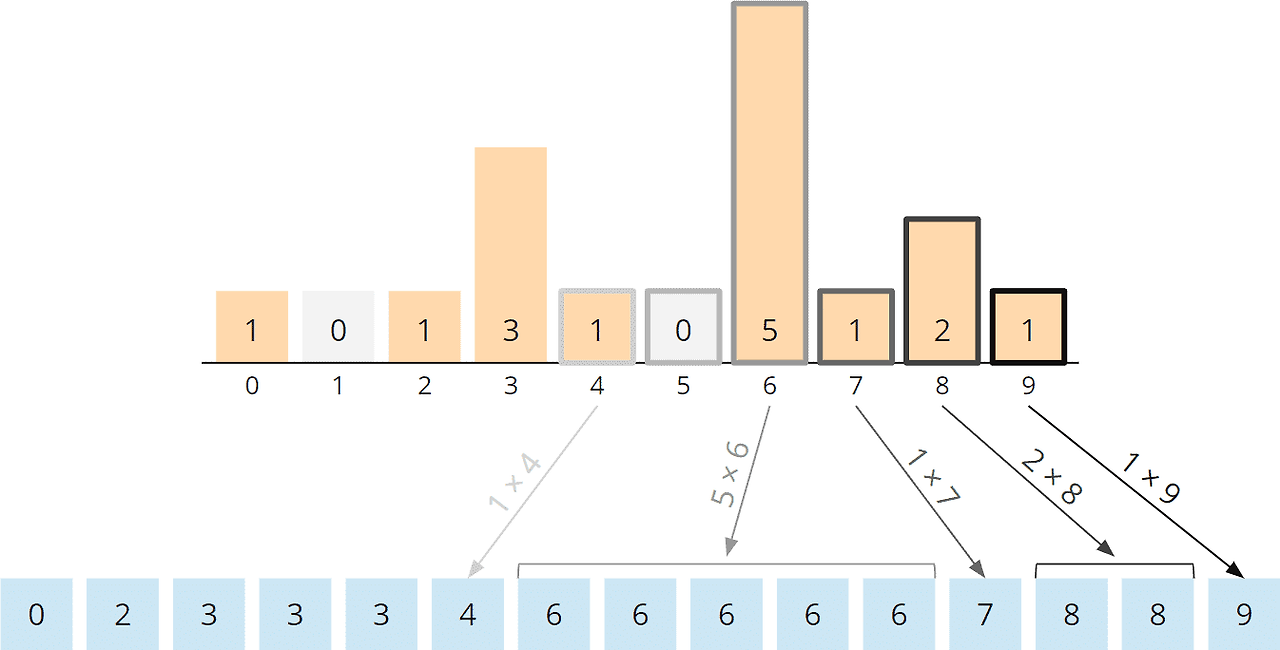
python code도 직관적이고 간단하다.
def counting_sort(list):
output = [0] * (len(list))
count = [0] * (max(list) + 1)
# count
for i in range(len(list)):
count[list[i]] += 1
# accumulation
start = 0
for i in range(len(count)):
end = start + count[i]
output[start:end] = [i] * count[i]
start = end
return output
Stable sort vs. Unstable sort
Summary

'Data Science' 카테고리의 다른 글
| [DSA 101] 3. Iteration vs. Recursion (0) | 2025.04.13 |
|---|---|
| [DSA 101] 2. Searching algorithm (0) | 2025.04.13 |
| [DSA 101] 1. Computation Complexity와 Big-O (0) | 2025.04.13 |
| Levenshtein distance (Edit distance) (4) | 2024.08.28 |



