[DSA] 2. Searching algorithm
이전글 : 2025.04.13 - [Data Science] - [DSA] 1. Computation Complexity와 Big-O [DSA] 1. Computation Complexity와 Big-OAlgorithm?(Generally) 어떤 문제를 해결하기 위한 일련의 계산 절차.(Computer science에서는) 컴퓨터 상에서
jae-walker.tistory.com
이전 글에서는 searching algorithm인 linear search와 binaray search에 대해 살펴보고, 각각의 time complexity가 어떻게 되는지 계산해 보았다. 또 다른 basic algorithm인 sorting으로 넘어가기 전, 잠깐 iteration과 recursion에 대해 짚고 넘어가 보려고 한다.
Search algorithm을 구현한 python code에서도 볼 수 있다시피, 대부분의 알고리즘은 기본적으로 어떤 동작을 반복적으로 수행하도록 만들어진다. (사실상 모든 알고리즘의 동작은 if-else와 for문이면 모두 구현할 수 있다고 해도 과언이 아님...!) 반복 수행을 구현하는 방식에 따라 알고리즘을 iteration과 recursion으로 나누기도 하는데, 이 두 방식의 차이점에 대해서 알아보자.
Iteration
- 정의 : 특정 조건 동안 일련의 연산을 반복해서 실행하는 방식으로 구현된 알고리즘.
- 구현방식 : for/while loop를 통해
- 변수 초기화
- 반복할 명령어 sequence (for, while loop 내부에 구현된 코드)
- loop 종료 조건 (for index의 범위, while의 조건)
- 무한반복에 빠지는 경우 : loop 종료 조건에 도달할 수 없을 때 loop가 무한히 실행된다. loop를 돌 때마다 변수에 새로운 값을 업데이트하기 때문에 memory를 추가적으로 계속 잡아 먹지는 않지만, CPU 사이클을 계속 사용하면서 멈추지 않는다.
Recursion (재귀)
- 정의 : 알고리즘이 자기자신과 똑같은 subproblem을 가지고 있는 형태로 구현된 알고리즘. 점화식을 떠올리면 쉽다!
- 구현방식 : 함수 내부에서 자기자신과 같은 함수를 반복 호출(recursive call)하는 방법을 통해
- Base case : 더이상 recursive call을 하지 않고 유일한 결과값을 반환할 수 있는 가장 간단한 case. 예를 들면, 값이 1개만 있는 list에서 특정 값을 찾는 것.
- General case : same problem in smaller scale을 호출하는 상위 함수.
- 종료 조건은 따로 정의하지 않고, recursive call이 base case에 도달한 뒤 모든 함수가 결과값을 반환하게 되면 종료.
- 무한재귀에 빠지는 경우 : Subproblem이 상위 problem보다 더 작은 scale이 아닌 경우 base case에 도달하지 못 하기 때문에 함수 call이 무한히 발생한다. 무한루프는 CPU 사이클만 계속 잡아먹지만, 무한재귀는 함수를 무한히 호출하기 때문에 stack overflow를 발생시키며 메모리를 터트린다...;;

Iteration vs. Recursion
사실 모든 반복되는 알고리즘은 두 가지 방법 모두로 구현할 수 있다. 다만, 기본적으로 같은 time complexity를 가지더라도 Iteration은 function 내부에서 변수만 업데이트하는 방식으로 연산하기 때문에 빠르고 메모리도 적게 쓰는 반면, Recursive는 함수를 반복해서 call 하기 때문에 속도도 느리고 메모리도 더 사용한다. 그렇다고 항상 iteration이 더 좋은 방식은 아니다. 경우에 따라 recursion을 사용하여 time complexity를 줄일 수 있는 알고리즘도 있기 때문에, 알고리즘 특성에 따라 선택적으로 사용하면 된다.
예시 1) Binary search
이전 글에서 다뤘던 binary search도 recursion으로 구현할 수 있다. 반띵하고 중앙값에 따라 소거하는 동작이 search range만 달라졌지 동일하게 반복되기 때문이다.
# Binary search with Iteration
def binary_search_iter(list, target):
# 변수 초기화
search_range_start = 0
search_range_end = len(list) - 1
while search_range_start <= search_range_end: # 종료 조건
# 반복할 연산
mid = (search_range_start + search_range_end) // 2
if list[mid] == target:
return mid
elif list[mid] < target:
search_range_start = mid + 1
else:
search_range_end = mid - 1
return -1
# Binary search with Recursion
def binary_search_recr(list, target, search_range_start, search_range_end):
if search_range_start > search_range_end:
return -1
else:
mid = (search_range_start + search_range_end) // 2
if list[mid] == target:
return mid
elif list[mid] < target:
return binary_search_recr(list, target, mid+1, search_range_end)
else:
return binary_search_recr(list, target, search_range_start, mid-1)- Time complexity를 따져 보면, 둘다 O(logN)이다. 딱히 recursion으로 구현하는 이점이 있지는 않은 것 같지만 recursion을 쉽게 적용해볼 수 있는 알고리즘의 예시 중 하나라고 보면 되겠다.
예시 2) 피보나치 수열
Recursion으로 구현하면 코드가 굉장히 간단해지는 예시도 있다. 피보나치 수열과 같이 점화식 형태로 문제를 정의할 수 있는 것들이다.

# Fibonacci with Iteration
def fibonacci_iter(n):
# 변수 초기화
prev = 0
curr = 1
result = 0
for i in range(n+1): # 종료조건
# 반복 계산
result = prev + curr
prev = curr
curr = result
return result
# Fibonacci with Recursion
def fibonacci_recr(n):
if n < 2: return n # Base case
return fibonacci_recur(n-1) + fibonacci_recur(n-2)- 피보나치 수열의 정의를 그대로 반영한 recursion 방식의 코드가 간단하고 가독성이 좋다.
- But, time complexity를 따져보면 recursion 방식에 문제가 있다는 걸 알 수 있다. f(6)을 구하기 위해서는 f(5)와 f(4)가 필요한데, f(5)를 구하기 위해서는 다시 f(4)와 f(3)이 필요하다. time complexity를 따져보면 상위 문제가 2개의 sub-problem으로 반복되어 분화하고, base case에 도달하는 데 max N만큼이 걸리므로 O(2^N)이다. 망했다.

출처 : https://medium.com/launch-school/recursive-fibonnaci-method-explained-d82215c5498e
예시 3) Combination (조합)
고등학교 확률통계 시간에 배웠던 그 조합. 서로 다른 n개의 원소에서 r개를 중복 없이, 순서를 고려하지 않고 선택할 수 있는 경우의수를 말한다.

이것도 점화식 형태로 간단히 나타낼 수 있고, 이를 Recursion 형태의 코드로 바로 옮길 수 있다.

# Combination with Recursion
def C(n, r):
if r > n:
return 0
elif r == 0 or r == n:
return 1
else:
return C(n-1, r-1) + C(n-1, r)
이 경우도 sub-problem이 중복되어 call 되고, 이에 따라 그 하위 problem도 모두 중복되어 call 된다.
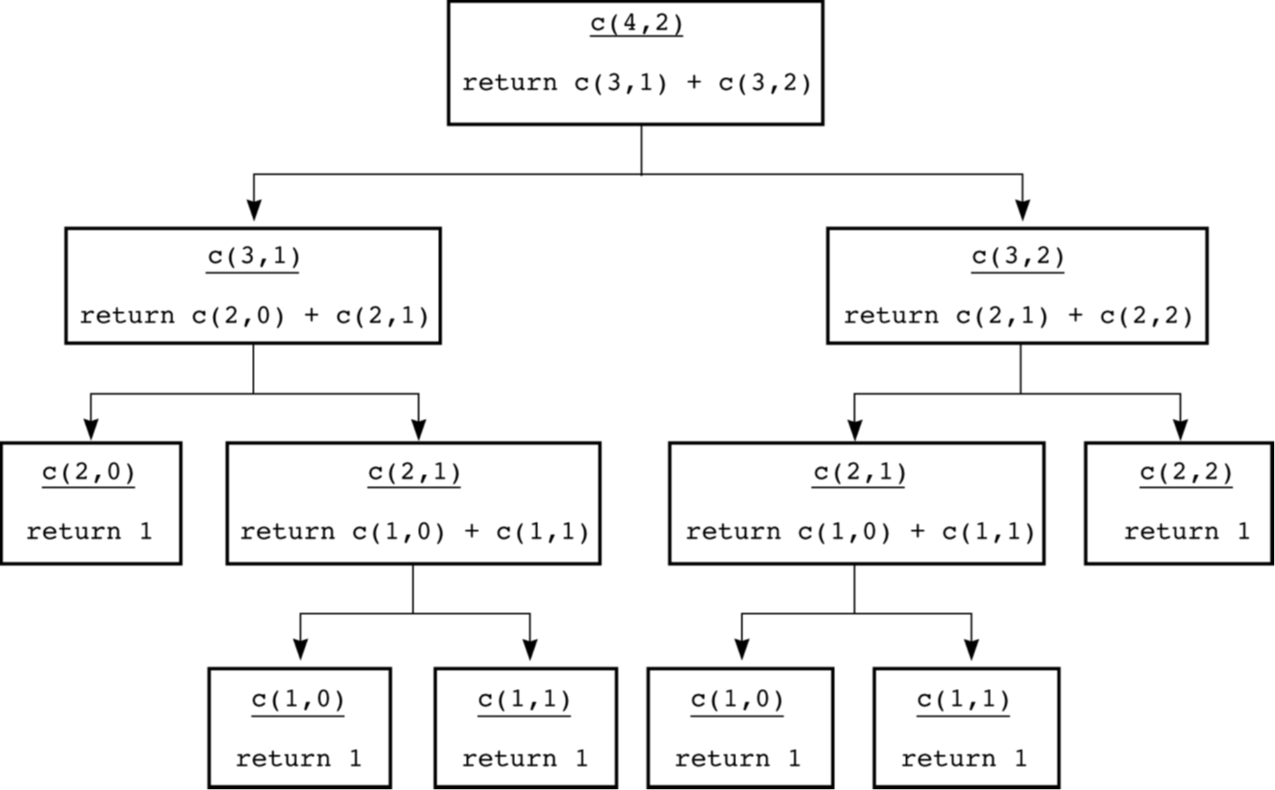
Overlapping subproblems (중복 부분 문제)
이렇게 하나의 problem이 여러 개의 독립적인 sub-problem으로 나뉘는 게 아니라, sub-problem이 중복된 tree처럼 퍼져나가는 형태를 띄는 문제를 overlapping sub-problem이라고 한다. 이 경우에는 단순히 순수 recursion만으로 구현하면 O(2^N)이라는 어마무시한 time complexity를 가지는 문제로 둔갑한다.
따라서, overlapping subproblem 여부에 따라 알고리즘을 구분해서 생각해 볼 필요가 있어진다.
Divide & Conquer vs. Dynamic programming
Sub-problem이 중복되지 않고 유일한 sub-problem으로 쪼개지는 알고리즘을 "Divide and Conquer (분할 정복)" 알고리즘이라고 한다. 뒤에서 다룰 Merge sort, Quick sort 등이 이에 해당한다.
한편, 피보나치, combination처럼 subproblem이 중복되는 문제를 해결하는 방법은 "Dynamic Programming"이라고 한다. 중복 연산이 여러 번 수행되는 것을 방지하기 위해, 문제를 풀기 위한 모든 unique sub-problem을 먼저 구한 후 결괏값을 저장해 놓고 가져다 쓰는 Memoization이나 Tabulation 등의 기법을 추가로 사용한다.
DP 관련한 내용은 나중에 기회가 되면 다른 포스팅에서 더 자세하게 다뤄보는 것으로 하고 일단 넘어간다.

Summary
- 반복 연산을 구현하는 방법에는 iteration과 recursion이 있다.
- 경우에 따라 Recursion으로 구현하는 것이 더 편한 알고리즘들이 있다. 대표적으로 점화식 형태를 띤 알고리즘들.
- 무한재귀를 막기 위해서는 항상 sub-problem의 scale이 상위 problem보다 작아야 하고, 더이상 recursive call을 하지 않는 base case가 존재해야 한다.
- 만약, overlapping sub-problem이 존재한다면 recursion 방식은 엄청한 비효율을 야기한다. 따라서, 이런 경우에는 iteration을 사용하던지, dynamic programming을 사용해야 한다.
⚠️ Disclaimer 혼자 공부한 것을 정리한 글이므로 잘못된 내용이 있을 수 있습니다.
틀린 내용이나 더 좋은 방법이 있는 경우, 댓글로 알려주시면 업데이트하겠습니다.
'Data Science' 카테고리의 다른 글
| [DSA 101] 4. Sorting (0) | 2025.04.15 |
|---|---|
| [DSA 101] 2. Searching algorithm (0) | 2025.04.13 |
| [DSA 101] 1. Computation Complexity와 Big-O (1) | 2025.04.13 |
| Levenshtein distance (Edit distance) (0) | 2024.08.28 |



