Algorithm?
- (Generally) 어떤 문제를 해결하기 위한 일련의 계산 절차.
- (Computer science에서는) 컴퓨터 상에서 돌아가는 program의 mathematical abstraction.
Efficiency of an Algorithm
- 어떤 문제를 해결하기 위한 방법이 딱 하나만 있는 것은 아니다. 그럼 우리는 어떤 알고리즘을 선택 or 개발해야 할까?
- 문제를 해결하기 위해 필요한 cost, 즉 "비용"이 적을수록 "좋은" 알고리즘이다. 같은 일을 하는데 월급도 적게 받고, 듀얼 모니터 사달라는 소리도 안하는 직원을 회사가 좋아하는 것 처럼... (심지어 컴퓨터는 박봉으로 영혼까지 빨아먹는다고 불평도 퇴사도 안한다! 안심하고 착취가 가능하다!!!) 그래서 좋은 Algorithm을 평가하는 가장 기본적인 기준은 2가지다.
- Time complexity : 얼마나 빨리 해내냐?
- Space complexity : 얼마나 적은 메모리 공간을 차지하면서 일하냐?
Complexity를 어떻게 측정할 수 있을까?
가장 직관적인 방법은 실제로 프로그램을 돌려서 실제 다 돌아가는데 걸리는 execution time과 사용된 메모리 양을 측정하는 방법을 떠올릴 수 있다. 일단 일을 시켜본 다음에 실제로 얼마나 걸리는지 보는 거다. 근데 이게 진짜 우리가 알고 싶은 알고리즘의 효율성을 제대로 평가하기는 어렵다. 그날따라 직원이 컨디션이 안 좋을 수도 있고, 일하는 데 필요한 자료들을 옆 부서에 요청했는데 늦게 줄 수도 있다. 컴퓨터도 마찬가지로 실제 실행시간은 알고리즘의 복잡도에만 영향을 받는 게 아니라, CPU 성능, 메모리에서 데이터를 읽어오는 속도 등등 다른 많은 factor들에 영향을 받는다. 더군다나 우리는 일을 안시켜보고도 이 놈이 일을 빠르게 잘 해내는 똘똘한 놈인지를 미리 알아보고 싶은 건데 실제 알고리즘을 다 구현해보고 실행시간을 보는 건 너무 비효율적이다.
그래서 우리는 좀 더 formal하고 간단한 방법으로 알고리즘의 time complexity를 표현해보기로 했다.
그게 바로 "Big-O notation"이다.
Big-O notation
- (Generally) 인수가 특정 값이나 무한대로 향할 대 함수의 극한 동작을 설명하는 수학적 표기법.
- (Computer science에서) 입력 크기가 커짐에 따라 실행 시간이나 공간 요구 사항이 어떻게 증가하는지 대략적인 수치로 근사하는 표기법.
수학적인 Big-O notation의 정의는... 복잡하니까 pass;; (궁금하신 분들은 https://en.wikipedia.org/wiki/Big_O_notation)
CS에서는 알고리즘을 복잡도를 적당히 분류할 수 있을 만큼만 간소화해서 사용한다. 이 동네에서의 Formal definition은 다음과 같다.
T(N) ∈ O(f(N))
모든 가능한 임의의 positive integer N에 대해서 T(N) < c * f(N)가 성립하는 f(N) 중 가장 작은 차수를 가지는 함수.
뭐라는 건지 아직도 감이 잘 안 온다면, 사실 이거만 기억하면 된다.
1. Time complexity를 다항식과 그 밖의 초월함수로 표현하되 (T(N)), 증가율이 가장 큰 항을 계수를 생략하고 표기한 것(O(f(N)))
2. 연산에 여러 가지 case가 존재한다면 worst-case만을 고려한다.
복잡해보일 수 있지만, 예시를 몇 가지 따라가다 보면 어렵지 않다. 어떤 문제를 해결하는데 필요한 총 연산의 갯수를 T(N)이라고 하자. (N은 data size)
T(N) = N^2 + 5N^5 --> 다항식의 최고차항를 찾고 계수 생략 --> O(N^5)
T(N) = 2N^2 + 3N --> 다항식의 최고차항을 찾고 계수 생략 --> O(N^2)
T(N) = 1/N + 100 --> 1/N = N^(-1), 100 = 100*N^0, 최고차항 = 100, 계수 생략 --> O(1)
T(N) = 100 cos(N) + 50N^2 --> cosine은 -1~1을 왔다갔다하는 함수이므로 N^2가 더 빠르게 증가 --> O(N^2)
T(N) = log N + 2N --> log는 N이 100늘어날 때 겨우 2 늘어남, 따라서 2N이 dominant --> O(N)
T(N) = 2^N + N^2 --> N=10 넣어보면, 2^N = 1025, N^2 = 100 --> O(2^N)
Big-O를 계산하다보면 많이 나오는 함수들은 몇 가지로 정해져 있다. 딱보면 얼마나 복잡한 놈인지 바로 알 수 있게 아래 그래프를 머릿 속에 넣어두는 게 좋겠다.
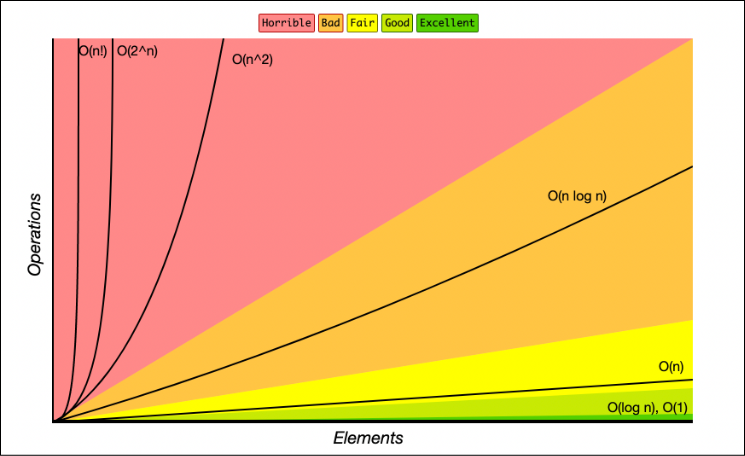
어떤 알고리즘을 만들었는데 O(1), O(log N) 이다? 오.. 이 놈 아주 빠릿빠릿한 놈이군 볼 수 있다. 일을 1개를 줘도 100개를 줘도 하루 ~ 일주일이면 다 끝내는 아주 초특급 에이스다. 우리 회사에 아주 큰 재산이다. 꼭 채용해서 열심히 굴려보자. O(N)도 뭐 나쁘지 않다. 일이 1개일 때는 하루, 100개 던져주면 차근차근 100일에 걸쳐 다 해내는 정직한 놈이다.
근데 O(2^N)인 놈이 나타났다...? 데이터 사이언스, 컴퓨터 공학에서 뭐든 exponential이 나오면 그냥 일단 최악이라고 생각하면 된다. 얘를 데려와 일을 시키느니 회사가 망하거나 지구가 멸망하는게 빠르다. 그래도 컴퓨턴데 계속 굴리면 언젠가 해오지 않을까 하는 안일한 생각은 접어두시길. 고작 데이터 100개를 처리하는데 2^100 = 126,7650,6002,2822,9401,4967,0320,5376이라는 어마무시한 시간이 걸린다. million, billion이 오가는 빅데이터 시대에 이런 알고리즘을 돌리겠다는 건 비유가 아니라 literally 지구 멸망을 기다리겠다는 걸로 볼 수 밖에 없다.
+) 어떤 고마운 분께서 보기좋게 data structure별로 Big-O cheatsheet을 만들어 두셨다.

⚠️ Disclaimer 혼자 공부한 내용을 정리한 글이므로 잘못된 내용이 있을 수 있습니다.
틀린 내용이나 더 좋은 방법이 있는 경우, 댓글로 알려주시면 업데이트하겠습니다.
'Data Science' 카테고리의 다른 글
| [DSA 101] 4. Sorting (0) | 2025.04.15 |
|---|---|
| [DSA 101] 3. Iteration vs. Recursion (0) | 2025.04.13 |
| [DSA 101] 2. Searching algorithm (0) | 2025.04.13 |
| Levenshtein distance (Edit distance) (4) | 2024.08.28 |



