[DSA] 1. Computation Complexity와 Big-O
Algorithm?(Generally) 어떤 문제를 해결하기 위한 일련의 계산 절차.(Computer science에서는) 컴퓨터 상에서 돌아가는 program의 mathematical abstraction. Efficiency of an Algorithm어떤 문제를 해결하기 위한 방법이
jae-walker.tistory.com
앞선 글에서 알고리즘은 어떤 문제를 해결하기 위한 일련의 계산 절차이며, 알고리즘의 complexity를 평가하기 위한 Big-O notation에 대해서 살펴보았다. 그럼 이제 몇 가지 알고리즘에 요걸 적용해보자.
Searching algorithm
먼저, 가장 간단한 searching algorithm이다.
Searching은 주어진 데이터 안에서 원하는 target 값을 찾아 그 위치를 반환해주는 동작이다. 예를 들어,
list = [1, 4, 6, -1, 5, -8, 12]
여기서 4를 찾아봐! 하면 index 1을 반환하고, -4를 찾아봐! 하면 없어!를 반환해야 한다.
이렇게 원하는 값을 찾는 방법은 여러 가지가 있는데 하나씩 살펴보며, 어떤 방법이 가장 complexity가 낮은 좋은 알고리즘인지를 확인해보자.
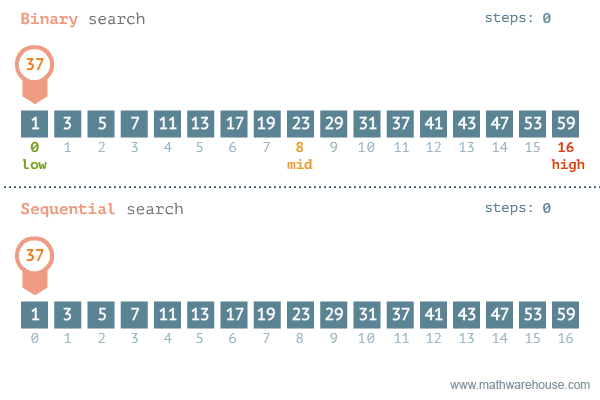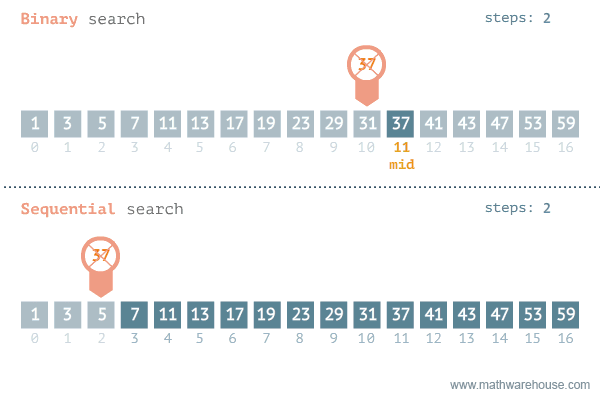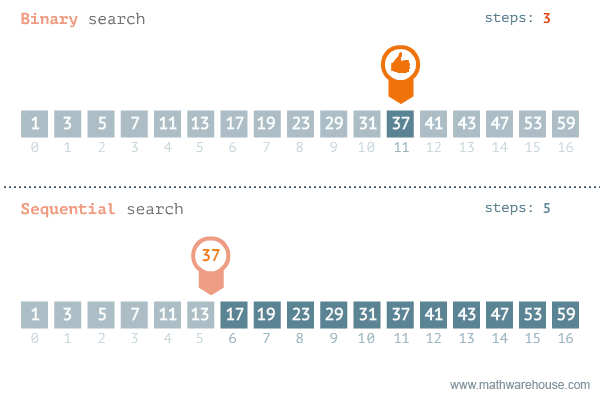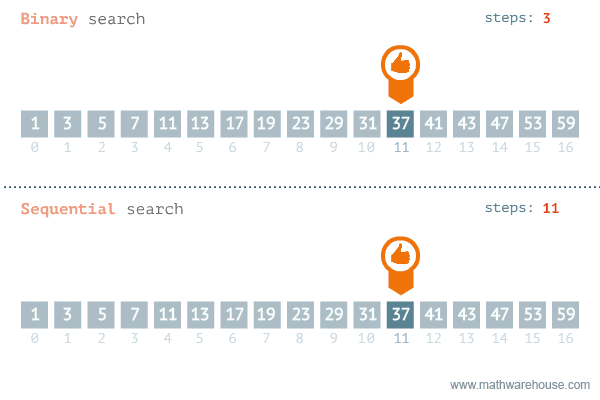
1. Linear Search
가장 간단한 방법은 앞에서부터 순서대로 하나씩 확인해보는 것이다.
list[0]을 꺼내온다. → 값이 맞는지 확인해본다. → 맞으면 index를 반환한다. 아니면 다음으로 넘어간다.
list[1]를 꺼내온다. → 값이 맞는지 확인해본다. → 맞으면 index를 반환한다. 아니면 다음으로 넘어간다.
...
를 찾을 때까지 반복한다.
python 코드로 구현하면 아래와 같다.
def linear_search(list, target):
for i in range(len(list)):
if list[i] == target:
return i
return -1
Time complexity
운이 좋게 첫번째 값이 내가 찾던 그 값이면 한 번만에 바로 찾을 수 있겠지만, 찾는 값이 list의 가장 마지막에 있는 worst case에서는 list의 크기 N만큼 위 동작을 반복해야 값을 찾을 수 있다. Big-O는 worst-case에 대해서만 고려한다고 했으니까, 이 경우에서 필요한 연산은 (꺼내오기, 값 비교, 다음 index로 넘어가기)가 모두 "N번"이 필요하다. 따라서, Big-O notation으로 time complexity를 나타내면 O(N)다.
2. Dictionary Search (a.k.a Binary Search)
만약 데이터가 "잘 준비"되어 있다면 Linear search보다 좀 더 빠르고 쉽게 찾을 수도 있다.
알고리즘의 이름에서 유추할 수 있듯이, 만약 값들이 사전처럼 ㄱ,ㄴ,ㄷ 순서대로, 혹은 숫자 크기 순서대로 잘 정리가 되어 있다면? 아무도 "zero"라는 단어의 뜻을 찾기 위해 사전의 맨 앞장부터 하나씩 확인하지는 않는다. z 부분의 어딘가를 랜덤으로 편 다음, zombie 어쩌구가 나오면 아 더 앞 부분에 있구나 하고, za어쩌구가 나오면 아 이것보다는 뒤구나 하면서 찾겠지. (아... 요즘엔 종이사전을 안 찾아봐서 이거 뭔 느낌인지 모르려나...)
아무튼, data가 어떤 순서대로 잘 정렬(sorting)되어 있다면, 어떤 지점을 잡아서 값을 확인한 다음, 이거보다 앞에 있을지 뒤에 있을지를 판단해서 아닌 범위을 소거하고 search 범위를 좁혀나가는 방식으로 더 빠르게 찾는 것이 가능하다. 이 때, 중간 지점을 기준으로 양쪽을 나누는 것이 어느 쪽으로 선택되던 balance가 맞아 효율적이므로, 보통 data length / 2인 중간값을 중심으로 나누기 때문에 binary search라고도 부른다.
sorted_list = [-8, -1, 1, 4, 5, 6, 12] # where's 5 in this sorted list
index 0~6의 중간인 data[3]을 꺼내온다. → data[3] = 4, target보다 작다. → index가 3보다 작은 값들은 모두 소거한다.
index 4~6의 중간인 data[5]을 꺼내온다. → data[5] = 6, target보다 크다. → index가 5보다 큰 값들은 모두 소거한다.
index 4만 남았다. data[4]를 꺼내온다. → data[4] = 5. 찾았다! → index 4를 반환한다.
linear search로 했으면 루프를 5번 돌았어야 했지만, binary search를 사용하면 3번 만에 찾을 수 있다.
python 코드로 구현하면 아래와 같다.
def binary_search(list, target):
search_range_start = 0
search_range_end = len(list) - 1
while search_range_start <= search_range_end:
mid = (search_range_start + search_range_end) // 2
if list[mid] == target:
return mid # 중간값이 target과 같으면 index를 반환
elif list[mid] < value:
search_range_start = mid + 1 # 중간값이 target보다 작으면, 중간값 아래는 소거
else:
search_range_end = mid - 1 # 중간값이 target보다 크면, 중간값 위는 소거
return -1 # 못 찾으면 -1 반환
Time complexity
흠... 이건 linear search처럼 딱 감이 안 올 수도 있다. search range는 그대로고 하나씩 반복해서 연산하면 되는 게 아니라 search range 자체가 변하기 때문이다. 그럼 반대로 생각하면 된다. 반띵하고 값 비교를 하는 연산이 언제 1번 추가될까? N값이 2배가 될 때! 2^N으로 값이 변할 때마다 linear하게 값이 증가하는 함수는 log. 따라서, binary search의 time complexity는 O(log_2 N)이다. log의 밑 또한 상수로 빼낼 수 있기 때문에 생략하면 O(log N)
Binary search처럼 일정한 비율로 처리해야 하는 N의 갯수가 반복해서 소거되는 알고리즘은 보통 O(log N)의 complexity를 가진다.
Summary
| Search algorithm | Time complexity | 전제조건 |
| Linear search | O(N) | 없음. 모든 data에서 가능. |
| Binary search | O(logN) | data가 sorted여야 사용 가능. |
마지막으로 Linear search와 Binary search 알고리즘을 잘 시각화해놓은 애니메이션을 첨부하며 마무우리이ㅣㅣ.
⚠️ Disclaimer 혼자 공부한 것을 정리한 글이므로 잘못된 내용이 있을 수 있습니다.
틀린 내용이나 더 좋은 방법이 있는 경우, 댓글로 알려주시면 업데이트하겠습니다.
'Data Science' 카테고리의 다른 글
| [DSA 101] 4. Sorting (0) | 2025.04.15 |
|---|---|
| [DSA 101] 3. Iteration vs. Recursion (0) | 2025.04.13 |
| [DSA 101] 1. Computation Complexity와 Big-O (0) | 2025.04.13 |
| Levenshtein distance (Edit distance) (4) | 2024.08.28 |



